개념
선택 정렬은 정렬되지 않은 데이터들에 대해 가장 작은 데이터를 찾아 가장 앞의 데이터와 교환해나가는 방식이다.
과정
- 주어진 리스트 중 최소값을 찾는다.
- 그 값을 맨 앞에 위치한 값과 교체한다. (패스(pass))
- 맨 처음 위치를 뺀 나머지 리스트를 같은 방법으로 교체한다.

과정 - 그림설명

1단계 : 첫 번째 자리를 기준 위치로 정하고, 전체 원소 중 가장 작은 원소인 2를 선택하여 자리를 교환한다.
2단계 : 두 번째 자리를 기준 위치로 정하고, 1번 위치를 제외한 나머지 원소 중 가장 작은 원소인 10과 교환한다.
3단계 : 세 번째 자리를 기준 위치로 정하고, 1번과 2번 위치를 제외한 나머지 원소 중 가장 작은 16과 교환한다.
4단계 : 네 번째 자리를 기준 위치로 정하고, 1번과 2번과 3번을 제외한 나머지 원소 중 가장 작은 30과 교환한다.
5단계 : 마지막 원소이므로 자동 정렬이 되었다. (4단계까지만 하면 된다.)
구현(C++)
#include <stdio.h>
int main()
{
int n, i, j, a[1001], temp, minIdx;
scanf("%d", &n); // 데이터의 개수 n을 정한다.
for (i = 0; i < n; i++) // n개만큼 데이터의 값을 받는다.
{
scanf("%d", &a[i]);
}
// 선택 정렬 시작
for (i = 0; i < n - 1; i++) // 마지막 값은 자동 정렬이 되었기에 비교할 필요가 없으므로 n-1번까지 반복한다.
{
minIdx = i; // 최소값 인덱스를 설정한다.
for (j = i + 1; j < n; j++) // 비교값을 반복하는 것이므로 i+1번위치에서 마지막위치인 n번까지 반복한다.
{
if (a[minIdx] > a[j]) // 만약 최소값인 a[minIdx]보다 비교값이 더 작을 때 비교값 인덱스를 기억한다.
{
minIdx = j;
}
}
// 비교가 끝났으므로 현재 위치값인 a[i]와 최소값인 a[minIdx]를 바꿔준다.
temp = a[i];
a[i] = a[minIdx];
a[minIdx] = temp;
}
// 선택 정렬 끝났으므로 출력한다.
for (i = 0; i < n; i++)
{
printf("%d ", a[i]);
}
return 0;
}
시간복잡도
n개의 데이터 개수가 있을 때, 2번의 for 루프로 정렬을 시킨다.
따라서 (n-1)만큼 반복하는데 그 안에서 (n-(i+1))만큼 또 반복하는데,
우리는 증가률에 따른 알고리즘 성능도를 예측하기에 고정 숫자인 상수를 제거한다면 n반복하는데 안에서 또 n만큼 반복한다고 볼 수 있다.
즉, O(n^2)로 표현할 수 있다.
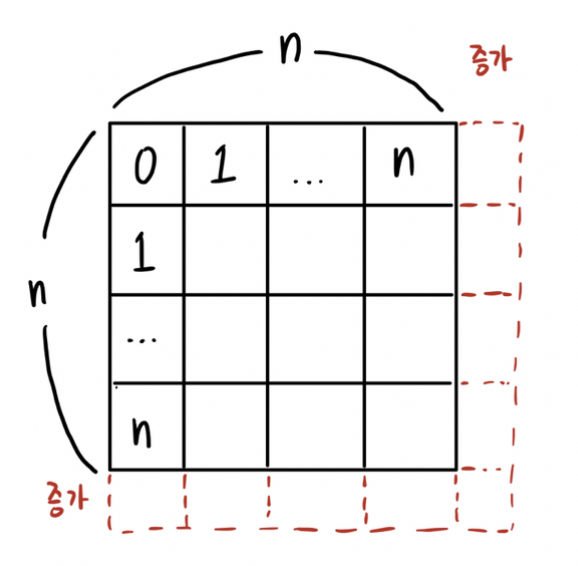
데이터 증가값이 위 그림처럼 된다고 생각하면 편하다.
n만큼 반복하면서 그 안에서 n만큼 반복하니까, 처리횟수가 n을 가로와 세로길이로 가지는 면적만큼 늘어나게 된다.
n이 증가할 때마다 가로와 세로 한 줄이 증가하므로 데이터가 커질수록 처리시간이 부담된다.

그래프로 그렸을 때는 위 그림처럼 처음에는 미미하지만 어느 순간부터 수직상승을 하는 것을 볼 수 있다.
정렬 비교
같은 시간 복잡도 O(n^2)를 가진 삽입 정렬(Insertion Sort), 버블 정렬(Bubble Sort)과 비교해보면
- 버블 정렬보다 교환 횟수가 적기에 항상 선택 정렬이 우수하다.
- 선택 정렬은 k번째 반복 후, k+1번째 요소를 찾기 위해 나머지 요소를 탐색하지만, 삽입 정렬은 필요한 만큼만 탐색하기에 훨씬 효율적으로 실행된다.
참고
https://ko.wikipedia.org/wiki/선택_정렬
https://terms.naver.com/entry.naver?docId=2270435&cid=51173&categoryId=51173
'코딩테스트 > 알고리즘' 카테고리의 다른 글
| 그리디 알고리즘(Greedy Algorithm)이란? (0) | 2022.07.15 |
|---|---|
| 삽입 정렬(Insertion Sort)이란? (0) | 2022.07.11 |
| 버블정렬(Bubble Sort)이란? (0) | 2022.07.10 |
| 시간복잡도 Big-O(빅오)란? (0) | 2022.05.17 |
